概览
-
sgn $$\mathrm{sgn}(x)=\left{\begin{align} & 1, & x>0 \ & 0, & x=0 \ & -1, & x<0\end{align}\right. $$
-
sigmoid $$\sigma(x)=\mathrm{sigmoid}(x)=\frac{1}{1+\exp(-x)}$$
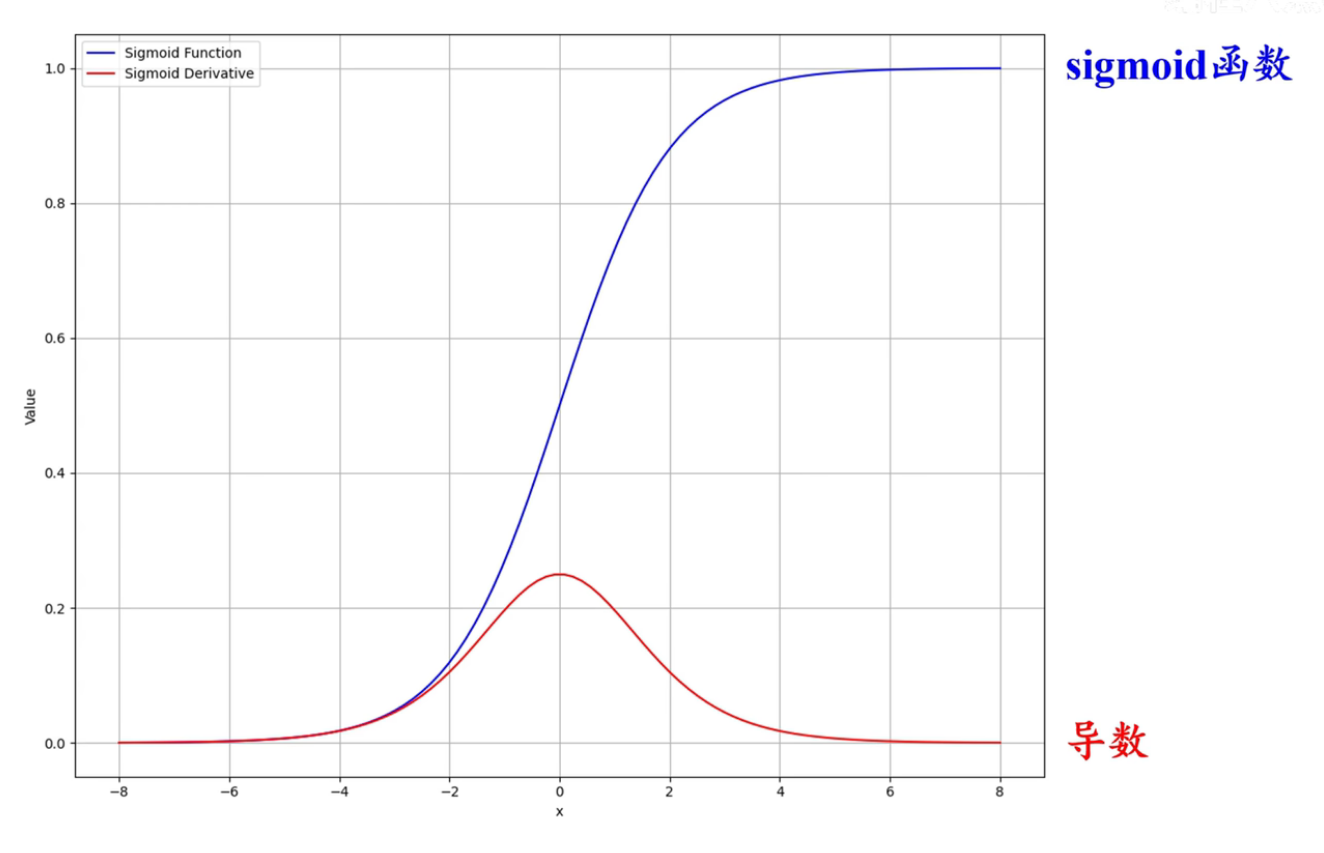
-
tanh $$\tanh (x)=\frac{1-\exp(-2x)}{1+\exp(-2x)}$$
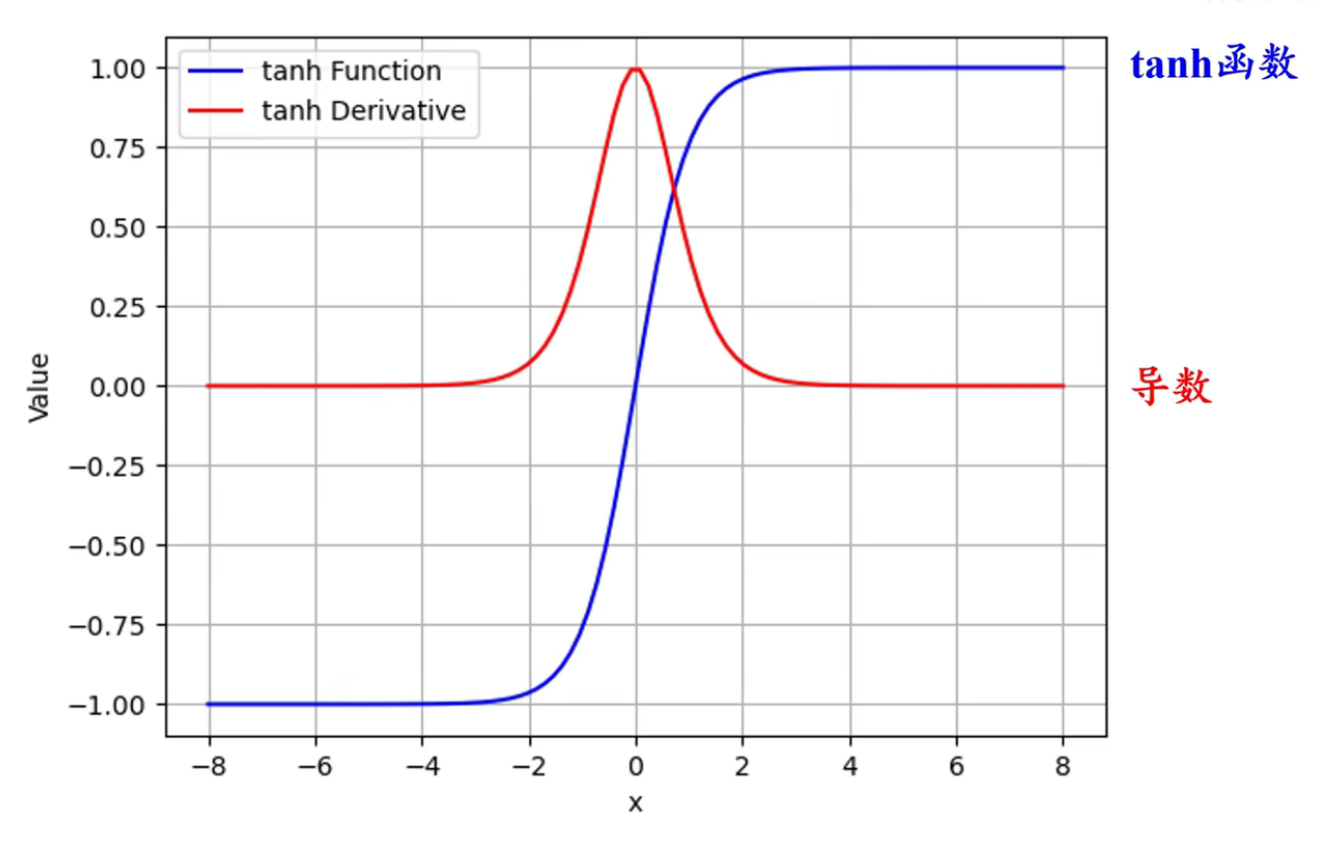
-
ReLU $$\mathrm{ReLU}(x)=\mathrm{max}(x,0)$$
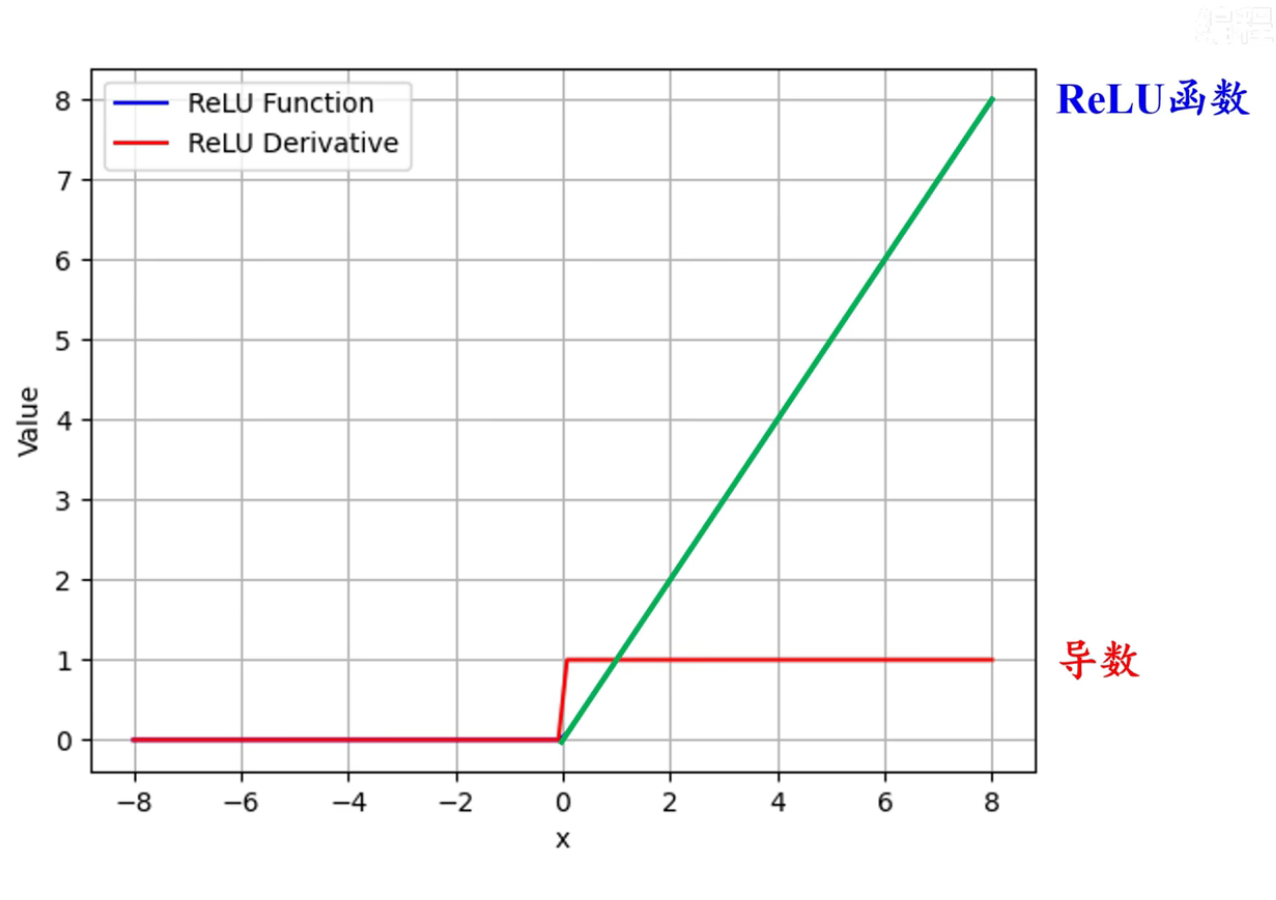
-
Leaky ReLU $$\mathrm{LeakyReLU}(x)=\left{\begin{align} & x, & x>0\ & \alpha x, & x\leq 0 \end{align}\right.$$ 其中 $\alpha$ 很小,$\to 0$,经验上 $\alpha=0.01$ 或者 $\alpha\sim N(0,1)$
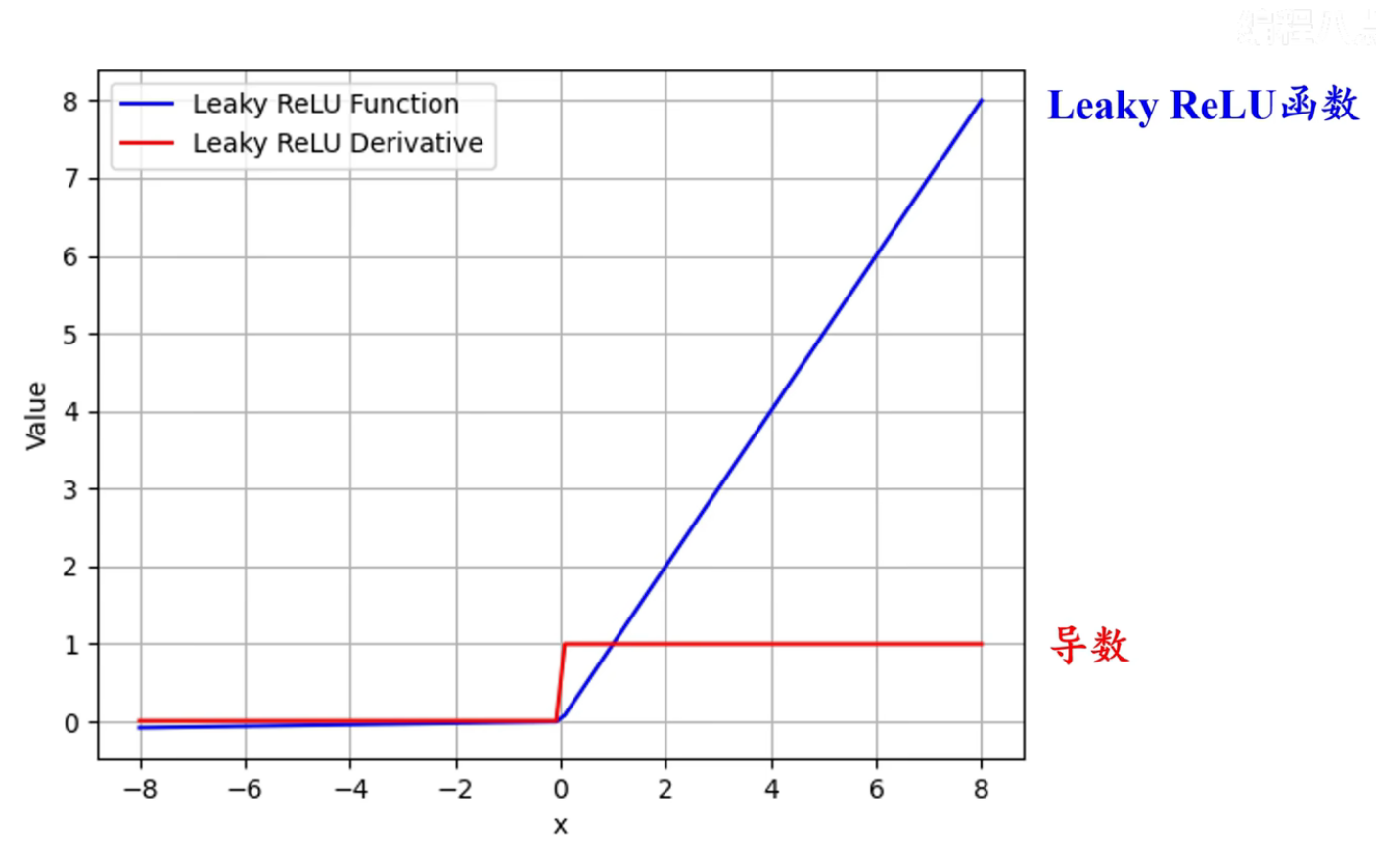
-
ELU $$\mathrm{ELU}(x)=\left{\begin{align} & x, & x>0 \ & \alpha(e^{x}-1), & x\leq 0\end{align}\right.$$
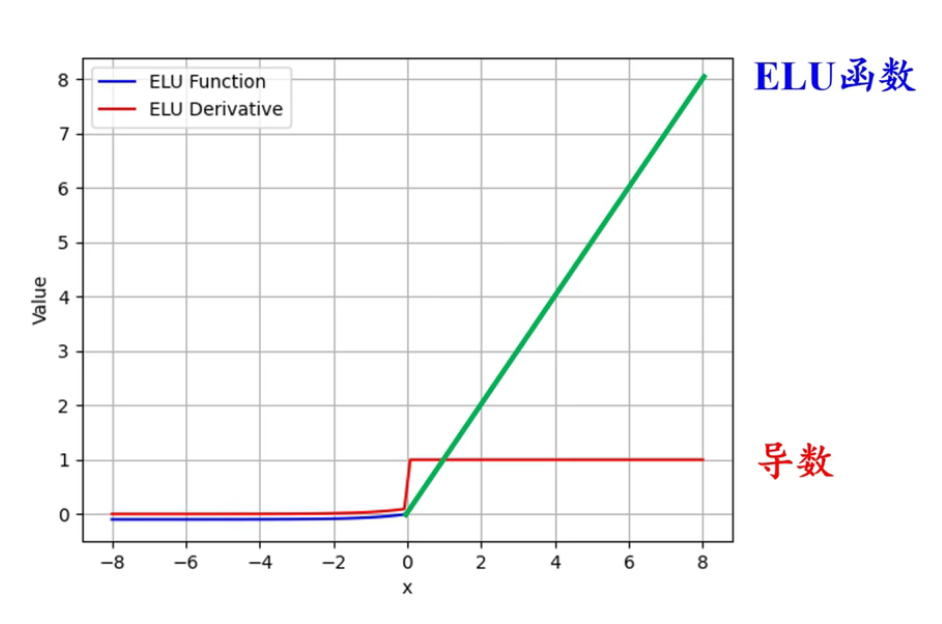
-
Swish $$\mathrm{Swish}(x)=x\cdot\sigma(\beta \cdot x)$$
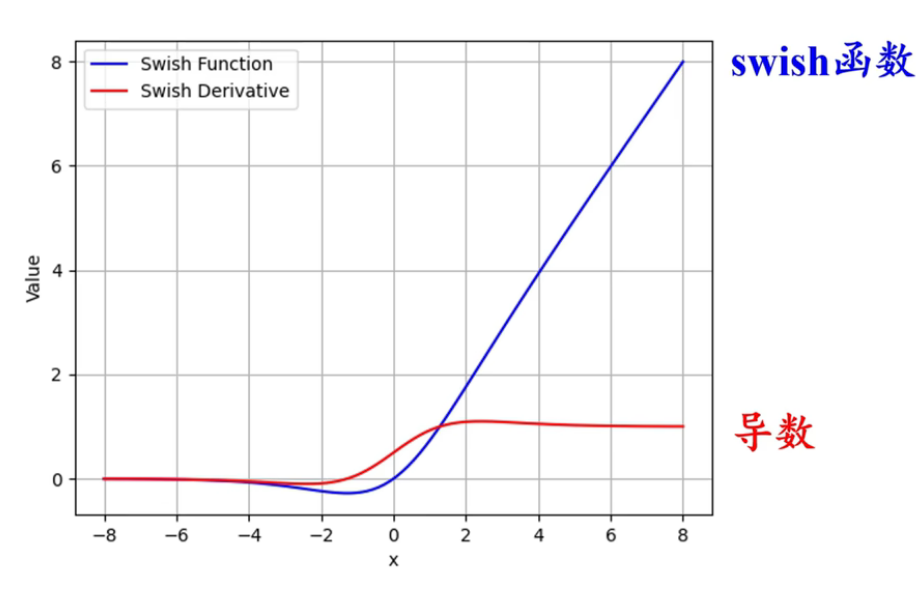
对比
| 激活函数 | 优点 | 缺点 |
|---|---|---|
| sigmoid | 单侧分布 双侧饱和 |
|
| tanh | 双侧分布 | 双侧饱和 |
| ReLU | 单侧饱和 | 未双侧分布 Dying ReLU |
| Leaky ReLU | 双侧分布 | |
| ELU | 单侧饱和 双侧分布 |
|
| Swish | 单侧饱和 双侧分布 |
梯度饱和
指激活函数某些域下梯度 $\to 0$ 的现象 导致梯度下降慢,模型收敛效果差,甚至失活
BP 失活
指梯度为 $0$, 梯度下降法 更新权重参数时为 $0$ 的现象
e.g. Dying ReLU
ReLU
LeakyReLU
随机 LeakyReLU
把 $\alpha$ 随机取值,总体上 $\alpha \sim N(0,1)$
PReLU
把 $\alpha$ 作为需要学习的参数