数字电路

卡诺图

最小项

对 $n$ 阶逻辑函数 $F(X_{1},X_{2},\dots,X_{n})$

一个

  • 包含所有 逻辑参数/逻辑参数反变量 有且仅有一次 的逻辑表达式 $:=$ 最小项

把最小项逻辑参数依次排列

  • 正变量 $\to 1$
  • 反变量 $\to 0$ 后得到的二进制数作为最小项序号
例子

对于三阶逻辑函数 $F(A,B,C)$

它的最小项包括

最小项 对应二进制数 最小项表达式
$A’B’C'$ $001$ $m_{1}$
$A’B’C$ $010$ $m_{2}$
$A’BC'$ $011$ $m_{3}$
$A’BC$ $011$ $m_{4}$
$AB’C'$ $100$ $m_{5}$
$AB’C$ $101$ $m_{6}$
$ABC'$ $110$ $m_{7}$
$ABC$ $111$ $m_{8}$

任何 $n$ 阶逻辑函数都可以由它的 $2^{n}$ 个最小项组合表示

$$ F_{n}(\dots)=\sum_{k=1}^{2^{n}}(0 / 1)\cdot m_{k} $$

最小项性质

  1. 全体最小项之和为 $1$
  2. 任意两个最小项之积为 $0$

卡诺图

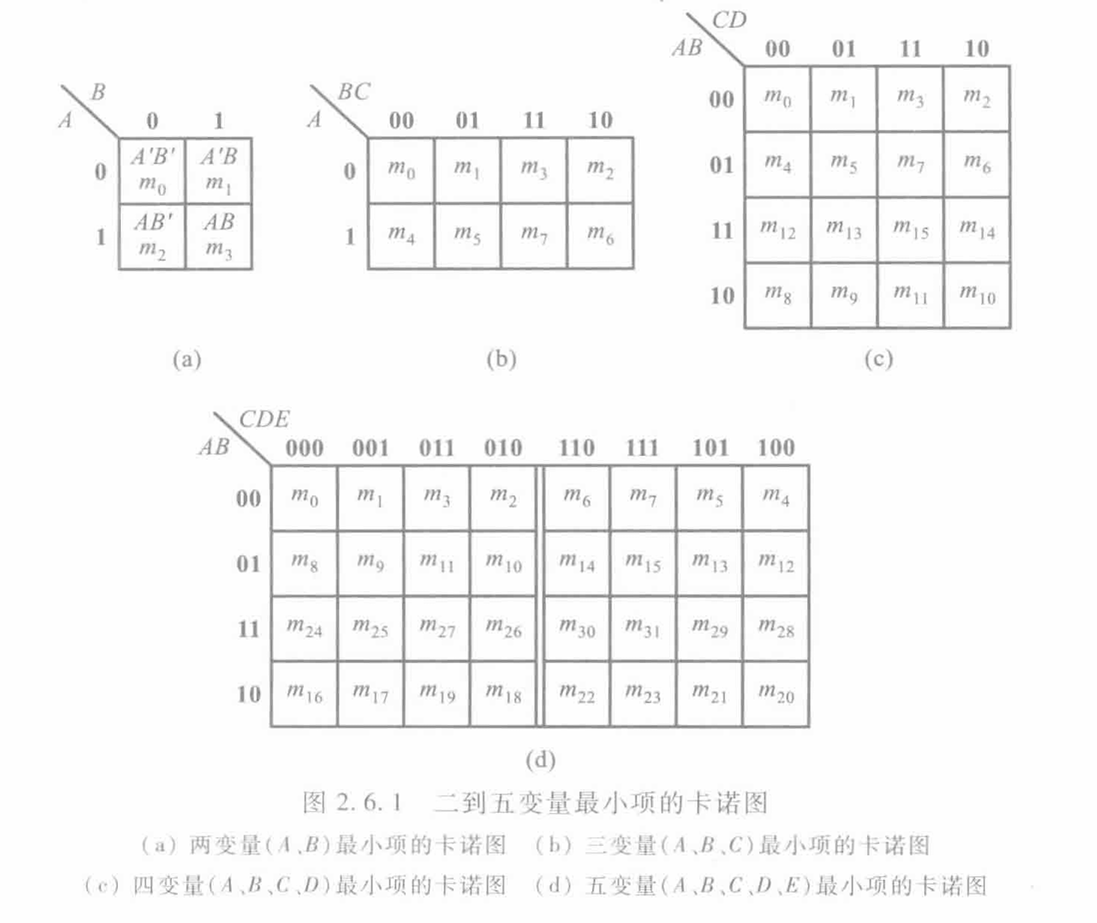
image.png

  1. 背下这张图，高于 5 阶的不要求手动化简
  2. 根据逻辑函数存在的最小项填表
    • 存在 $\to 1$
    • 不存在 $\to 0$
为什么排序不按大小序

保证图中相邻最小项满足逻辑相邻

逻辑相邻 $:=$ 两个最小项

  • 有且只有一个变量，在一项中为正，另一项为反
  • 其他最小项相同

⭐ 卡诺图的边界也是相邻的

如何记忆卡诺表序

  1. 一阶：完美大小序 0 1
  2. 二阶：大小序调换第三和第四
  3. 三阶：
  4. 左半边 0xx，右半边 1xx
  5. 0xx 与二阶一致
  6. 1xx 同 0xx 的 xx 关于中线镜像对称

化简逻辑函数

  1. 构建 卡诺图 > 卡诺图
  2. 找到面积为 $2^{n}$ 的尽可能大的任意形状矩形，其内部全是 $1$
尽可能大的矩形

如果矩形可以合并，说明不够大

所以建议从大往小找，即 $\dots \to 16 \to 8 \to 4 \to 2$

  1. 重复 2. 直到框住图中所有 $1$
矩形可以跨边界

注意卡诺图的边界是相邻的

所以矩形可以跨边界

比如 $2\times 2$ 矩形可以是图的四个角

  1. 写出 3. 中的所有矩形代表的逻辑项
快速得到对应逻辑项

  1. 先看列后看行
  2. 框中行/列有不一样的参数被消去
  3. 行&列得到的结果取乘积
  1. 得到最简结果
化简结果不具有唯一性

步骤 3. 的方案不是唯一的

这也导致化简结果不是唯一

实际上逻辑函数的化简结果本来就不唯一

化简带无关项的逻辑函数

已知

  • 逻辑函数 $\sum m(\dots)$
  • 约束项 $\sum d(\dots)$

则

  1. 参照 卡诺图 > 化简逻辑函数
  2. 约束项中的最小项用 “$\times$” 填入图中
  3. “$\times$” 可以被圈，也可以不被圈