齐次坐标

相对于三维坐标 $(x,y,z)$ 引入第四维 $(x,y,z,w)$

若 $w=0$ 则 $(x,y,z,0)$ 是一个方向
若 $w = 1$ 则 $(x,y,z,1)$ 是一个位置

引入齐次坐标主要是为了坐标变换都能表示成 $矩阵\times向量$ 的统一形式

坐标变换

约定已知

待变换向量为 $\boldsymbol{v}=(x,y,z,1)$
待变换方向为 $\boldsymbol{w}=(x,y,z,0)$
待变换坐标为 $\boldsymbol{x}=(x,y,z,w)$

平移变换

$$ T=\begin{bmatrix} 1 & 0 & 0 & X \ 0 & 1 & 0 & Y \ 0 & 0 & 1 & Z \ 0 & 0 & 0 & 1 \end{bmatrix} $$

$$ T(\boldsymbol{v}) =\begin{bmatrix} 1 & 0 & 0 & X \ 0 & 1 & 0 & Y \ 0 & 0 & 1 & Z \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \ y \ z \ 1 \end{bmatrix} = \begin{bmatrix} x+X \ y+Y \ z+Z \ 1 \end{bmatrix} $$ $$ T(\boldsymbol{w}) =\begin{bmatrix} 1 & 0 & 0 & X \ 0 & 1 & 0 & Y \ 0 & 0 & 1 & Z \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \ y \ z \ 0 \end{bmatrix}
=\begin{bmatrix} x \ y \ z \ 0 \end{bmatrix} $$

缩放变换

$$ S=\begin{bmatrix} X & 0 & 0 & 0 \ 0 & Y & 0 & 0 \ 0 & 0 & Z & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} $$ $$ S(\boldsymbol{x})=\begin{bmatrix} X & 0 & 0 & 0 \ 0 & Y & 0 & 0 \ 0 & 0 & Z & 0 \ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \ y \ z \ w \end{bmatrix}

\begin{bmatrix} Xx \ Yy \ Zz \ w \end{bmatrix} $$

旋转变换

比较复杂

旋转的实现方式有两种

旋转方式	四元数 Quaternion	欧拉角 Euler Angle
速度性能	faster ✅	fast
易懂性	good	better ✅
用途	引擎核心	用户接口

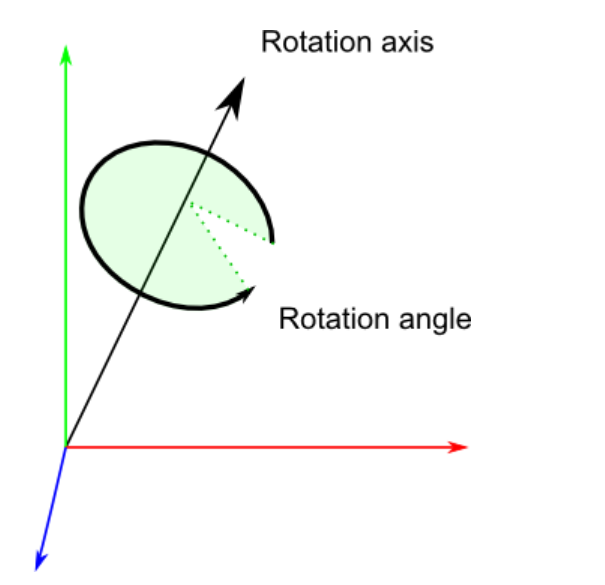
四元数

四元数 $\boldsymbol{q}=(x,y,z,w)$ where.

1
2
3
4


x = RotationAxis.x * sin(RotationAngle / 2) 
y = RotationAxis.y * sin(RotationAngle / 2) 
z = RotationAxis.z * sin(RotationAngle / 2) 
w = cos(RotationAngle / 2)

复合变换

最终的三种变换的复合变换为：

$$ M\boldsymbol{x}=TRS\boldsymbol{x} $$ 三种变换矩阵顺序不可变

MVP Matrix

Model Matrix

模型在其模型文件中的坐标就是初始的 Model Coordinate

根据坐标变换中的复合变换就可以把它变换到世界坐标系下的位置，也就是 World Coordinate

该变换用到的矩阵就是 Model Matrix

View Matrix

再把世界坐标下的模型，通过复合变换转移到相对 camera 的坐标系下，得到 Camera Coordinate

该变换用到的矩阵就是 View Matrix

Projection Matrix

再通过一个 Project Matrix 让物体符合人眼的视锥体视觉

Before	After

实现：

1
2
3
4
5
6
7


// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective( 
	glm::radians(FoV), // The vertical Field of View, in radians: the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in) 
	4.0f / 3.0f, // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar? 
	0.1f, // Near clipping plane. Keep as big as possible, or you'll get precision issues. 
	100.0f // Far clipping plane. Keep as little as possible. 
);

整体实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// Projection matrix: 45° Field of View, 4:3 ratio, display range: 0.1 unit <-> 100 units 
glm::mat4 Projection = glm::perspective(glm::radians(45.0f), (float) width / (float)height, 0.1f, 100.0f); 

// Or, for an ortho camera: 
// glm::mat4 Projection = glm::ortho(-10.0f,10.0f,-10.0f,10.0f,0.0f,100.0f); // In world coordinates 

// Camera matrix 
glm::mat4 View = glm::lookAt( glm::vec3(4,3,3), 
	// Camera is at (4,3,3), in World Space glm::vec3(0,0,0), 
	// and looks at the origin glm::vec3(0,1,0) 
	// Head is up (set to 0,-1,0 to look upside-down) );
	
// Model matrix: an identity matrix (model will be at the origin) 
glm::mat4 Model = glm::mat4(1.0f); 
	
// Our ModelViewProjection: multiplication of our 3 matrices 
glm::mat4 mvp = Projection * View * Model; 
	// Remember, matrix multiplication is the other way around