一种运用 自动机闭包 从 自动机 > NFA 构造 自动机 > DFA 的形式化构造方法
- 从初始状态 $p_{0}$ 开始,把 $p_{0}$ 放入集合 $NS$
- 对 $NS$ 每个未操作元素进行操作: 对所有条件 $\delta$ 做 $\delta-\mathrm{clossure}\left{ p_{k} \right}$ 的结果放入 $NS$
- 直到 $NS$ 不产生新状态结束
- 把 $NS$ 中的所有状态分别记作新的状态 $S_{k}$
- $\left{ S \right}$ 和 $\left{ \delta \right}$ 构成新的 自动机 > DFA
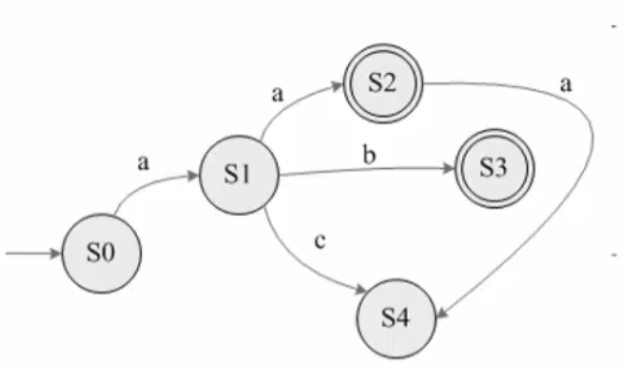
例子
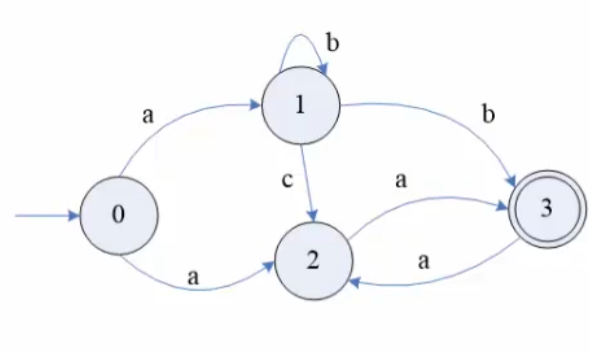
| 新状态机状态 | 当前状态 | a-clossure | b-clossure | c-clossure | NS |
|---|---|---|---|---|---|
| $S_{0}$ | { 0 } | { 1, 2 } | $\emptyset$ | $\emptyset$ | { 1, 2 } |
| $S_{1}$ | { 1, 2 } | { 3* } | { 1, 3* } | { 2 } | { 3* }, { 1, 3* }, { 2 } |
| $S_{2}$ | { 3* } | { 2 } | $\emptyset$ | $\emptyset$ | { 1, 3* }, { 2 } |
| $S_{3}$ | { 1, 3* } | $\emptyset$ | { 1, 3* } | $\emptyset$ | { 2 } |
| $S_{4}$ | { 2 } | { 3* } | $\emptyset$ | $\emptyset$ | $\emptyset$ |