恒等变换

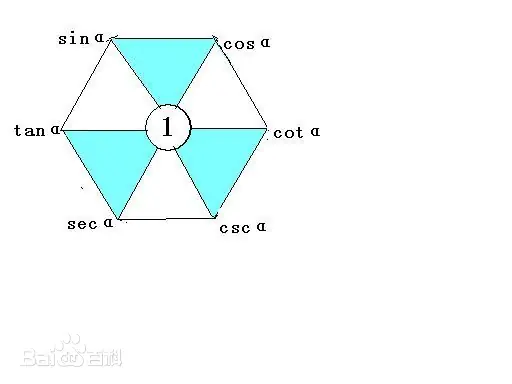
• 位置：上弦中切下割
• 对角原则：六边形中对角乘积为 1
  • $\sin x \cdot \csc x = 1$
  • $\cos x \cdot \sec x = 1$
  • $\tan x \cdot \cot x = 1$
• 倒三角原则：阴影/倒三角的上二顶点平方和等于下顶点
  • $\sin ^{2}x + \cos ^{2}x = 1$
  • $\tan ^{2}x + 1 = \sec ^{2}x$
  • $\cot ^{2}x + 1=\csc ^{2}x$
• 邻点原则：相邻顶点乘积等于当前顶点
  • $\sin x = \cos x \cdot \tan x$
  • $\cos x = \sin x\cdot \cot x$
  • $\tan x=\sin x\cdot \sec x$
  • $\sec x=\tan x\cdot \csc x$
  • $\csc x=\sec x\cdot \cot x$
  • $\cot x=\csc x\cdot \cos x$

积分

1. $\sec ^{2}x=1+\tan ^{2}x$
2. $\sec ^{2}x\mathrm{d}x=\mathrm{d}\tan x$
3. $\sin ^{2}\alpha-\sin ^{2}\beta=\sin(\alpha+\beta)\sin(\alpha-\beta)$
4. 1. $\frac{\sin x}{1-\cos x}=\cot\frac{x}{2}$
   2. $\frac{\sin x}{1+\cos x}=\tan\frac{x}{2}$

和差 & 积

!三角函数の和差与积

离散和