数字电路

编码器

二进制编码器

普通编码器

以 8线-3线编码器 为典型

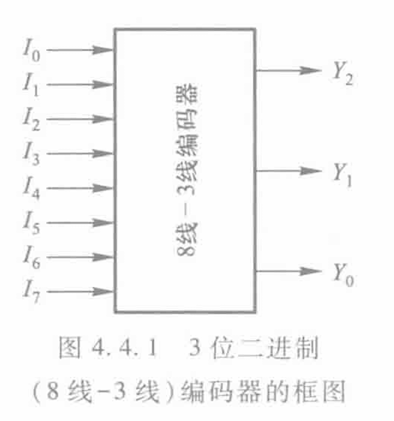
image.png

  • 操作
    • $I_{k}=1$ $\to$ $(k){2}=(\overline{Y{2}Y_{1}Y_{0}})_{2}$
    • 多个 $I_{k}$ 同时为 $1$ 行为未定义
  • 逻辑函数表达 $$\left{ \begin{align} Y_{2} & =\sum I(4,5,6,7) \ Y_{1} & =\sum I(2,3,6,7) \ Y_{0} & =\sum I(1,3,5,7) \end{align} \right. $$ 实则就是输出二进制位在哪些十进制数为 $1$

优先编码器

以 74HC148 为典型

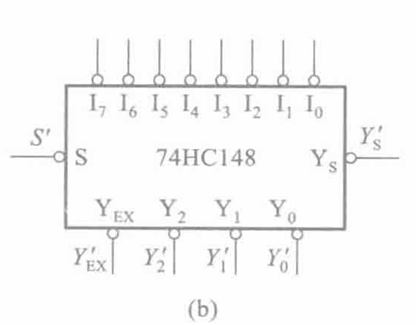
image.png

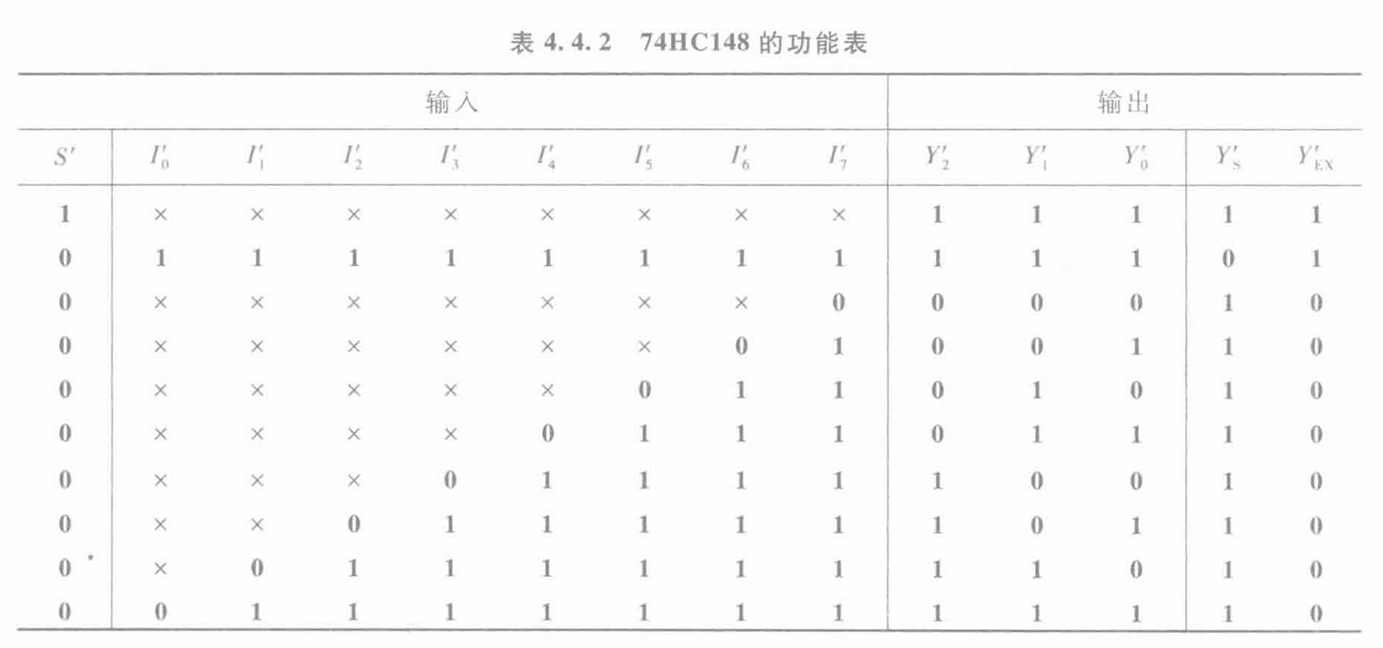
  • 功能表 image.png
    • 先按优先级 $I_{7}’>I_{6}’>I_{5}’>I_{4}’>I_{3}’>I_{2}’>I_{1}’>I_{0}’$ 选中输入
    • 根据选中输入，以 $(I_{8-k}’){\mathrm{74HC148}}=(I){83}$ 按照 普通编码器 得到输出 (类"十进制转二进制")
74HC148 低电平有效特性

处于物理特性、历史包袱等原因，74HC148 是低电平有效元件

所以直接代入 原input 到 普通编码器 时要注意反相！！

即 $(I_{8-k}’){\mathrm{74HC148}}=(I){83}$

二-十进制编码器

以 74HC137 为典型 aka 8421BCD

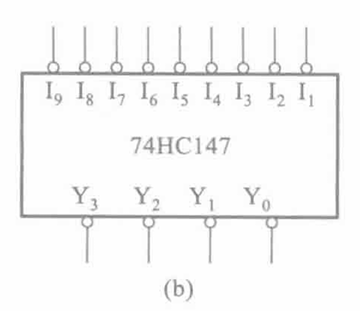
image.png

  • 操作
    • $I_{k}’=1$ $\to$ $(k){10}=(\overline{Y{3}‘Y_{2}‘Y_{1}‘Y_{0}’})_{2}$