离散冲激阶跃

• 离散单位冲激信号

  $$ \delta[n]=\left{ \begin{align} & 1, & n=0 \ & 0, & n\neq 0 \end{align} \right. $$

• 离散单位阶跃信号 $$ u[n]=\left{ \begin{align} & 1, & n\geq 0 \ & 0, & n<0 \end{align} \right. $$

连续冲激阶跃

• 连续单位冲激信号 定义困难，因为按照经典微积分观点得到 $\delta(0)=\infty$ 但总的来说 $$\int_{-\infty}^{+\infty} \delta(t) , \mathrm{d}t=1 $$ 可以根据以下逼近得到定义

  • 矩形面积定义 $$\delta(t)=\lim_{ \varepsilon \to 0 } \frac{1}{\varepsilon}\mathrm{rect}\left( \frac{t}{\varepsilon} \right)$$ (图示中用单位长度指向 $y$ 轴正方向的箭头表示逼近矩形)

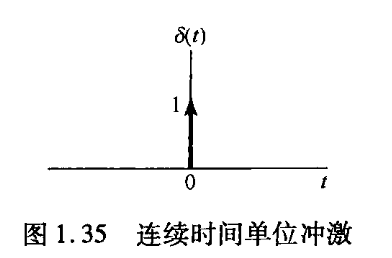
  • 高斯函数逼近 $$\delta(t)=\lim_{ \sigma \to 0 } \frac{1}{\sqrt{ 2\pi }\sigma}\exp \left{ {-\frac{t^{2}}{2\sigma^{2}}} \right}$$

• 连续单位阶跃函数 $$ u(t)=\left{ \begin{align} & 1, & t\geq 0 \ & 0, & t<0 \end{align} \right. $$